40. Perpetually offering to exchange or to sacrifice is a draw.
(See examples in Diagram 101 through 104)
Diagram 101: Red (in Capital) moves first
R8+1 r1+3
R8-3 r1-2
R8+2 r1-3
R8+3 r1+2
R8-2 ....
Explanation:
Red keeps trying to exchange or sacrifice the Rook. Since the Black
Rook is free to move, Red does not violate the rule and this game can
be a draw.
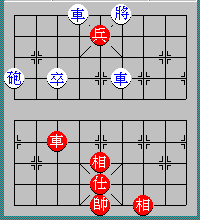Diagram 102: Red (in Capital) moves first
R73 r67
R32 r78
R24 r86
R41 r69
R12 r98
....
.
.
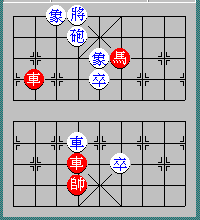Diagram 103: Red (in Capital) moves first
R8-3 r4-1
R8+1 r4-2
R8+2 r4-3
R8-3 ....
Explanation:
In Diagrams 102 and 103 neither side violates the rule and the games
can be ruled as draws.
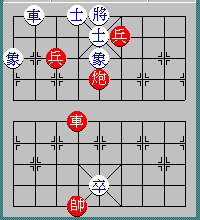Diagram 104: Red (in Capital) moves first
P78 r23
P87 r32
P78 r23
P87 r32
P78 ....
Explanation:
The Black Rook perpetually threatens to checkmate and the Red Pawn
perpetually tries to sacrifice. Neither side violates the rule
and the game is a draw.
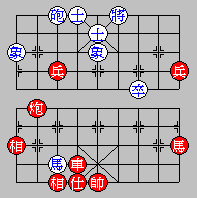Appendix: Example of Perpetual Chase
P76 m1+3
P67 m3-1
P78 m5+3
P87 m3-5
P76 ....
Explanation:
Red keeps moving its Pawn to keep the Black Knight "unprotected".
This constitutes the Red Rook perpetually chasing the unprotected
Black Knight. Red is violating the rule.
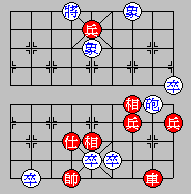Example of Non-Perpetual Chase
R2+1 c8+1
R2-1 c8-1
R2+1 c8+1
R2-1 c8-1
R2+1 ....
Explanation:
Each of Red Rook's move is threatening the Black Cannon but the
Black Cannon does not try to escape or seek for protection.
This is not a perpetual chase and does not violate the rule.
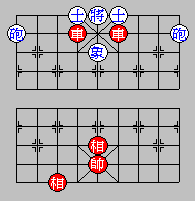Example of Mutual Perpetual Chase
R4-2 g4+5
R4+2 g5-4
R6-4 g4+5
R6+4 g5-4
R4-2 g4+5
R4+2 g5-4
R6-4 g4+5
....
Explanation
Red's R4-2 is to allow the Rook on the 6th file to chase
the Black's Cannon on the 9th file. In the next move, R4+2, Red
is using the Rook on the 4th file to chase the Black Cannon on the
9th file. This is two pieces perpetually chasing a piece.
As to the Black side, each time it moves the Guard it is threatening
the Red Rook on the 6th file with a Cannon. This is a perpetual chase.
Since both sides violate the rule, the game will be a draw if neither
side wants to change its move.