24. Chasing the same type of pieces
- Rook chases Rook:
- If both side can capture the other side, this is considered perpetual
sacrifice and should be ruled as a draw.
If one side cannot capture the other for some reason, the other
side cannot perpetually chases it.
- Cannon chases Cannon:
- If both side can capture the other side, this is considered perpetual
sacrifice and should be ruled as a draw.
If one side cannot capture the other for some reason, the other
side cannot perpetually chases it.
- Knight chases Knight:
- If both side can capture the other side, this is considered perpetual
sacrifice and should be ruled as a draw.
If one side is blocked, the other side cannot perpetually chases it.
(See examples in Diagram 51 to 55)
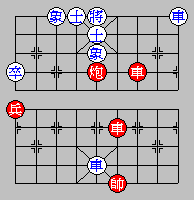
Diagram 51: Red (in Capital) moves first
R31 r98
R12 r87
R23 r78
R32 r89
R21 r97
R13 ...
.
.
Diagram 52: Red (in Capital) moves first
R8+2 r5+3
R8-3 r5-2
R8+2 r5+2
R8-2 r5-1
R8+1 ....
Explanation:
In Diagrams 51 and 52, the Red Rook perpetually sacrifices and
Black can capture it but, due to the circumstance, does not
want to. The game should be a draw.
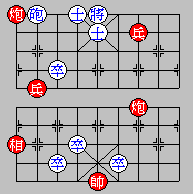Diagram 53: Red (in Capital) moves first
C38 c23
C87 c32
C78 c23
C87 c32
C78 ...
Explanation:
The Black Cannon cannot capture the Red Cannon. What Red is doing
is perpetual chase instead of perpetual threatening to checkmate.
Red has to change.
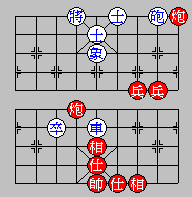Diagram 54: Red (in Capital) moves first
C72 c87
C23 c78
C32 c87
C23 c78
C32 ...
Explanation:
Although the Black Cannon is confined to the King's row,
Red cannon's attack on it is not a perpetual chase because
in one of Black Cannon's moves it is protected.
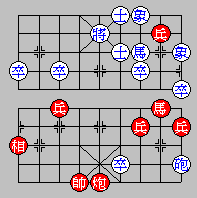Diagram 55: Red (in Capital) moves first
N2+4 n7+9
N4-2 n9-7
N2+4 n7+9
N4-2 n9-7
Explanation:
The Black knight is blocked, therefore, the Red knight is perpetually
chasing the Black knight. Red has to change.